職高高二數學教案
作為一位杰出的教職工,有必要進行細致的教案準備工作,教案有助于順利而有效地開展教學活動。快來參考教案是怎么寫的吧!下面是小編幫大家整理的職高高二數學教案,歡迎閱讀與收藏。
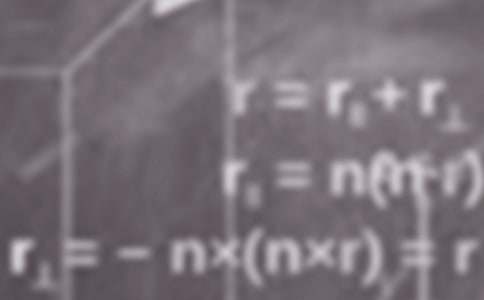
職高高二數學教案1
教學目標
(1)掌握圓的標準方程,能根據圓心坐標和半徑熟練地寫出圓的標準方程,也能根據圓的標準方程熟練地寫出圓的圓心坐標和半徑.
(2)掌握圓的一般方程,了解圓的一般方程的結構特征,熟練掌握圓的標準方程和一般方程之間的互化.
(3)了解參數方程的概念,理解圓的參數方程,能夠進行圓的普通方程與參數方程之間的互化,能應用圓的參數方程解決有關的簡單問題.
(4)掌握直線和圓的位置關系,會求圓的切線.
(5)進一步理解曲線方程的概念、熟悉求曲線方程的方法.
教學建議
教材分析
(1)知識結構
(2)重點、難點分析
①本節內容教學的重點是圓的標準方程、一般方程、參數方程的推導,根據條件求圓的方程,用圓的方程解決相關問題.
②本節的'難點是圓的一般方程的結構特征,以及圓方程的求解和應用.
教法建議
(1)圓是最簡單的曲線.這節教材安排在學習了曲線方程概念和求曲線方程之后,學習三大圓錐曲線之前,旨在熟悉曲線和方程的理論,為后繼學習做好準備.同時,有關圓的問題,特別是直線與圓的位置關系問題,也是解析幾何中的基本問題,這些問題的解決為圓錐曲線問題的解決提供了基本的思想方法.因此教學中應加強練習,使學生確實掌握這一單元的知識和方法.
(2)在解決有關圓的問題的過程中多次用到配方法、待定系數法等思想方法,教學中應多總結.
(3)解決有關圓的問題,要經常用到一元二次方程的理論、平面幾何知識和前邊學過的解析幾何的基本知識,教師在教學中要注意多復習、多運用,培養學生運算能力和簡化運算過程的意識.
(4)有關圓的內容非常豐富,有很多有價值的問題.建議適當選擇一些內容供學生研究.例如由過圓上一點的切線方程引申到切點弦方程就是一個很有價值的問題.類似的還有圓系方程等問題.
教學設計示例
圓的一般方程
教學目標:
(1)掌握圓的一般方程及其特點.
(2)能將圓的一般方程轉化為圓的標準方程,從而求出圓心和半徑.
(3)能用待定系數法,由已知條件求出圓的一般方程.
(4)通過本節課學習,進一步掌握配方法和待定系數法.
教學重點:(1)用配方法,把圓的一般方程轉化成標準方程,求出圓心和半徑.
(2)用待定系數法求圓的方程.
教學難點:圓的一般方程特點的研究.
教學用具:計算機.
教學方法:啟發引導法,討論法.
教學過程:
【引入】
前邊已經學過了圓的標準方程
把它展開得
任何圓的方程都可以通過展開化成形如
①
的方程
【問題1】
形如①的方程的曲線是否都是圓?
師生共同討論分析:
如果①表示圓,那么它一定是某個圓的標準方程展開整理得到的我們把它再寫成原來的形式不就可以看出來了嗎?運用配方法,得
②
顯然②是不是圓方程與是什么樣的數密切相關,具體如下:
(1)當時,②表示以為圓心、以為半徑的圓;
(2)當時,②表示一個點;
(3)當時,②不表示任何曲線.
總結:任意形如①的方程可能表示一個圓,也可能表示一個點,還有可能什么也不表示.
圓的一般方程的定義:
當時,①表示以為圓心、以為半徑的圓,
此時①稱作圓的一般方程.
即稱形如的方程為圓的一般方程.
【問題2】圓的一般方程的特點,與圓的標準方程的異同.
(1)和的系數相同,都不為0.
(2)沒有形如的二次項.
圓的一般方程與一般的二元二次方程
③
相比較,上述(1)、(2)兩個條件僅是③表示圓的必要條件,而不是充分條件或充要條件.
圓的一般方程與圓的標準方程各有千秋:
(1)圓的標準方程帶有明顯的幾何的影子,圓心和半徑一目了然.
(2)圓的一般方程表現出明顯的代數的形式與結構,更適合方程理論的運用.
【實例分析】
例1:下列方程各表示什么圖形.
(1) ;
(2) ;
一、教學內容分析
向量作為工具在數學、物理以及實際生活中都有著廣泛的應用.
本小節的重點是結合向量知識證明數學中直線的平行、垂直問題,以及不等式、三角公式的證明、物理學中的應用.
二、教學目標設計
1、通過利用向量知識解決不等式、三角及物理問題,感悟向量作為一種工具有著廣泛的應用,體會從不同角度去看待一些數學問題,使一些數學知識有機聯系,拓寬解決問題的思路.
2、了解構造法在解題中的運用.
三、教學重點及難點
重點:平面向量知識在各個領域中應用.
難點:向量的構造.
四、教學流程設計
五、教學過程設計
一、復習與回顧
1、提問:下列哪些量是向量?
(1)力(2)功(3)位移(4)力矩
2、上述四個量中,(1)(3)(4)是向量,而(2)不是,那它是什么?
[說明]復習數量積的有關知識.
二、學習新課
例1(書中例5)
向量作為一種工具,不僅在物理學科中有廣泛的應用,同時它在數學學科中也有許多妙用!請看
例2(書中例3)
證法(一)原不等式等價于,由基本不等式知(1)式成立,故原不等式成立.
證法(二)向量法
[說明]本例關鍵引導學生觀察不等式結構特點,構造向量,并發現(等號成立的充要條件是)
例3(書中例4)
[說明]本例的關鍵在于構造單位圓,利用向量數量積的兩個公式得到證明.
二、鞏固練習
1、如圖,某人在靜水中游泳,速度為km/h.
(1)如果他徑直游向河對岸,水的流速為4 km/h,他實際沿什么方向前進?速度大小為多少?
答案:沿北偏東方向前進,實際速度大小是8 km/h.
(2)他必須朝哪個方向游才能沿與水流垂直的方向前進?實際前進的速度大小為多少?
答案:朝北偏西方向前進,實際速度大小為km/h.
三、課堂小結
1、向量在物理、數學中有著廣泛的應用.
2、要學會從不同的角度去看一個數學問題,是數學知識有機聯系.
四、作業布置
1、書面作業:課本P73,練習8.4 4
職高高二數學教案2
一、教學目標
1、了解函數的單調性和奇偶性的概念,把握有關證實和判定的基本方法、
(1)了解并區分增函數,減函數,單調性,單調區間,奇函數,偶函數等概念、
(2)能從數和形兩個角度熟悉單調性和奇偶性、
(3)能借助圖象判定一些函數的單調性,能利用定義證實某些函數的單調性;能用定義判定某些函數的奇偶性,并能利用奇偶性簡化一些函數圖象的繪制過程、
2、通過函數單調性的證實,提高學生在代數方面的推理論證能力;通過函數奇偶性概念的形成過程,培養學生的觀察,歸納,抽象的能力,同時滲透數形結合,從非凡到一般的數學思想、
3、通過對函數單調性和奇偶性的理論研究,增學生對數學美的體驗,培養樂于求索的精神,形成科學,嚴謹的研究態度、
二、教學建議
(一)知識結構
(1)函數單調性的概念。包括增函數、減函數的定義,單調區間的`概念函數的單調性的判定方法,函數單調性與函數圖像的關系、
(2)函數奇偶性的概念。包括奇函數、偶函數的定義,函數奇偶性的判定方法,奇函數、偶函數的圖像、
(二)重點難點分析
(1)本節教學的重點是函數的單調性,奇偶性概念的形成與熟悉、教學的難點是領悟函數單調性,奇偶性的本質,把握單調性的證實、
(2)函數的單調性這一性質學生在初中所學函數中曾經了解過,但只是從圖象上直觀觀察圖象的上升與下降,而現在要求把它上升到理論的高度,用準確的數學語言去刻畫它、這種由形到數的翻譯,從直觀到抽象的轉變對高一的學生來說是比較困難的,因此要在概念的形成上重點下功夫、單調性的證實是學生在函數內容中首次接觸到的代數論證內容,學生在代數論證推理方面的能力是比較弱的,許多學生甚至還搞不清什么是代數證實,也沒有意識到它的重要性,所以單調性的證實自然就是教學中的難點、
(三)教法建議
(1)函數單調性概念引入時,可以先從學生熟悉的一次函數,二次函數、反比例函數圖象出發,回憶圖象的增減性,從這點感性熟悉出發,通過問題逐步向抽象的定義靠攏、如可以設計這樣的問題:圖象怎么就升上去了?可以從點的坐標的角度,也可以從自變量與函數值的關系的角度來解釋,引導學生發現自變量與函數值的的變化規律,再把這種規律用數學語言表示出來、在這個過程中對一些關鍵的詞語(某個區間,任意,都有)的理解與必要性的熟悉就可以融入其中,將概念的形成與熟悉結合起來、
(2)函數單調性證實的步驟是嚴格規定的,要讓學生按照步驟去做,就必須讓他們明確每一步的必要性,每一步的目的,非凡是在第三步變形時,讓學生明確變換的目標,到什么程度就可以斷號,在例題的選擇上應有不同的變換目標為選題的標準,以便幫助學生總結規律、
函數的奇偶性概念引入時,可設計一個課件,以的圖象為例,讓自變量互為相反數,觀察對應的函數值的變化規律,先從具體數值開始,逐漸讓在數軸上動起來,觀察任意性,再讓學生把看到的用數學表達式寫出來、經歷了這樣的過程,再得到等式時,就比較輕易體會它代表的是無數多個等式,是個恒等式、關于定義域關于原點對稱的問題,也可借助課件將函數圖象進行多次改動,幫助學生發現定義域的對稱性,同時還可以借助圖象(如)說明定義域關于原點對稱只是函數具備奇偶性的必要條件而不是充分條件、
職高高二數學教案3
教學目的:
1、使理解線段的垂直平分線的性質定理及逆定理,掌握這兩個定理的關系并會用這兩個定理解決有關幾何問題。
2、了解線段垂直平分線的軌跡問題。
3、結合教學內容培養學生的動作、形象和抽象。
教學重點:
線段的垂直平分線性質定理及逆定理的引入證明及運用。
教學難點:
線段的垂直平分線性質定理及逆定理的關系。
教學關鍵:
1、垂直平分線上所有的點和線段兩端點的距離相等。
2、到線段兩端點的距離相等的所有點都在這條線段的垂直平分線上。
教 具:投影儀及投影膠片。
教學過程:
一、提問
1、角平分線的性質定理及逆定理是什么?
2、怎樣做一條線段的垂直平分線?
二、新課
1、請同學們在練習本上做線段AB的垂直平分線EF(請一名同學在黑板上做)。
2、在EF上任取一點P,連結PA、PB量出PA=?,PB=?引導學生觀察這兩個值有什么關系?
通過學生的觀察、分析得出結果 PA=PB,再取一點P'試一試仍然有P'A=P'B,引導學生猜想EF上的所有點和點A、點B的距離都相等,再請同學把這一結論敘述成命題(用幻燈展示)。
定理:線段的垂直平分線上的點和這條線段的兩個端點的距離相等。
這個命題,是我們通過作圖、觀察、猜想得到的,還得在理論上加以證明是真命題才能做為定理。
已知:如圖,直線EF⊥AB,垂足為C,且AC=CB,點P在EF上
求證:PA=PB
如何證明PA=PB學生分析得出只要證RTΔPCA≌RTΔPCB
證明:∵PC⊥AB(已知)
∴∠PCA=∠PCB(垂直的定義)
在ΔPCA和ΔPCB中
∴ΔPCA≌ΔPCB(SAS)
即:PA=PB(全等三角形的對應邊相等)。
反過來,如果PA=PB,P1A=P1B,點P,P1在什么線上?
過P,P1做直線EF交AB于C,可證明ΔPA P1≌PB P1(SSS)
∴EF是等腰三角型ΔPAB的頂角平分線
∴EF是AB的垂直平分線(等腰三角形三線合一性質)
∴P,P1在AB的垂直平分線上,于是得出上述定理的逆定理(啟發學生敘述)(用幻燈展示)。
逆定理:和一條線段兩個端點距離相等的點,在這條線段的垂直平分線上。
根據上述定理和逆定理可以知道:直線MN可以看作和兩點A、B的距離相等的所有點的集合。
線段的垂直平分線可以看作是和線段兩個端點距離相等的所有點的集合。
三、舉例(用幻燈展示)
例:已知,如圖ΔABC中,邊AB,BC的垂直平分線相交于點P,求證:PA=PB=PC。
證明:∵點P在線段AB的`垂直平分線上
∴PA=PB
同理PB=PC
∴PA=PB=PC
由例題PA=PC知點P在AC的垂直平分線上,所以三角形三邊的垂直平分線交于一點P,這點到三個頂點的距離相等。
四、小結
正確的運用這兩個定理的關鍵是區別它們的條件與結論,加強證明前的分析,找出證明的途徑。定理的作用是可證明兩條線段相等或點在線段的垂直平分線上。
【職高高二數學教案】相關文章:
中職高二班主任工作計劃12-08
職高學習總結12-07
職高學習總結10-24
職高實習報告12-03
職高學生評語06-03
職高二年級班主任工作計劃范文12-19
職高的英語學期隨筆02-25
職高生評語07-05
職高簡歷自我評價12-05