關于“極值”,大家或許感覺對它的了解是足夠的,隨口就可以說出:極值是局部的最值。事實上,它還有很多你沒有注意到的細節,或許你只是“霧里看花,水中望月”而已,下面,小編為大家梳理極值的相關知識,了解你不知道的極值。
1、 極值的定義
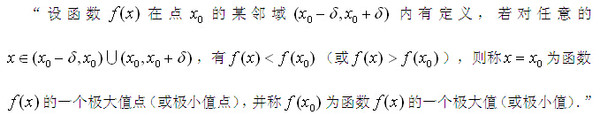
從定義可以看出,一個點想要稱為是極值點,唯一的要求就是此點處的函數值比它左鄰域及右鄰域內的函數值都要大(極大值)或者都要小(極小值),至于此點處函數的性態,比如連續性、可導性,并未做要求。換句話說,一個點是極值點,那么這個點可能是連續點,也可能是間斷點,還可能是不可導點。另外,作為一個極值點,要求它的左右兩側鄰域內都有定義,所以,極值點是不可能取在區間端點處的,這是和最值點的一個重要區別。
2、 極值的必要條件
必要條件表明(1)、可導的極值點必是駐點;(2)、可疑的極值點包含兩類:駐點與不可導點。那么,由此引申,極值點一定是駐點,錯!駐點一定是極值點,錯!
3、 極值的充分條件
第一充分條件
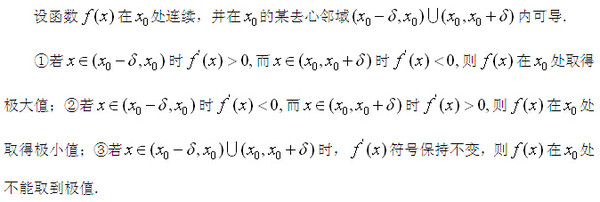
一句話,第一充分條件告訴我們,可疑的極值點中哪些才是真正的極值點?就是那些一階導函數在左右鄰域變號的才是。這一點想必大家都清楚,但是既然是充分條件,那么說明,一階導函數在左右鄰域變號的是極值點,但是極值點的左右鄰域內一階導函數未必變號,大家是否注意到了呢?你能舉出反例嗎?
第二充分條件

第二充分條件與第一充分條件相比,優勢在于操作簡便,缺點在于只能判別駐點是否為極值,不可導點處是否為極值是判定不出的。另外,第二充分條件要求大家都會證明,順便復習了極限的局部保號性。
通過這篇文章希望同學們能體會,在第一遍基礎學習的時候我們一定要把知識學細,學透,不留任何疑問,這樣厚實的基礎,一定會在二階方法的學習時形成強大的后勁!