商高的數學故事小學生手抄報

時間：2022-07-30 04:06:07 數學手抄報我要投稿

相關推薦

商高的數學故事小學生手抄報

　　商高是我國古代周朝著名的數學家，是勾股定理的創始人。至于他的生卒年月無

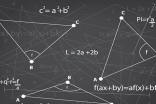
商高的數學故事小學生手抄報

　　從考查。商高的數學成就主要是勾股定理與測量術。上期講到的《墨經》是中國古代對幾何學理論研究的經典，而商高對幾何命題(勾股定理)的證明卻是獨樹一幟的。

　　勾股定理是一條很古老的定理，幾乎所有的數學古國，像埃及、巴比倫、希臘、印度都是很早就知道它了，小朋友，你們到初中后就能學到了。現在接觸一點這方面的知識，有利于以后的學習。西方通常稱勾股定理為畢達哥拉斯定理，那是因為他們把這個定理的最早發現，歸功于畢達哥拉斯。是不是他最早發現這個定理的呢?其實很難肯定。我國古代有部《周髀算經》，內容十分豐富，著重講述了數學在天文學方面的應用。據這部著作記載，大約在公元前11世紀商高就有了關于勾股定理的知識，如是這樣，就要比畢達哥拉斯早500年!

　　勾股定理的證明方法有500余種。其中商高的證明方法十分簡捷。證明的基本思想是把復雜的平面幾何問題，歸結為研究平面圖形的面積，然后通過對面積的代數運算而完成對幾何問題的證明，是一種幾何代數化的思想，這種思想方法很值得我們學習。

【商高的數學故事小學生手抄報】相關文章：