數學三角函數教學設計
三角形中的三角函數式
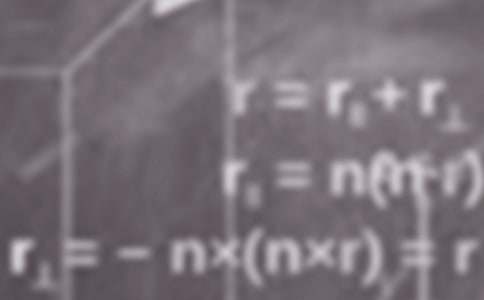
三角形中的三角函數關系是歷年高考的重點內容之一,本節主要幫助考生深刻理解正、余弦定理,掌握解斜三角形的方法和技巧。
●難點磁場
已知△ABC的三個內角A、B、C滿足A+C=2B. ,求cos 的值。
難點 不等式的證明策略
不等式的證明,方法靈活多樣,它可以和很多內容結合。高考解答題中,常滲透不等式證明的內容,純不等式的證明,歷來是高中數學中的一個難點,本難點著重培養考生數學式的變形能力,邏輯思維能力以及分析問題和解決問題的能力。
●難點磁場
已知a>0,b>0,且a+b=1。
難點 解不等式
不等式在生產實踐和相關學科的學習中應用廣泛,又是學習高等數學的重要工具,所以不等式是高考數學命題的重點,解不等式的應用非常廣泛,如求函數的定義域、值域,求參數的取值范圍等,高考試題中對于解不等式要求較高,往往與函數概念,特別是二次函數、指數函數、對數函數等有關概念和性質密切聯系,應重視;從歷年高考題目看,關于解不等式的內容年年都有,有的是直接考查解不等式,有的則是間接考查解不等式。
●難點磁場
解關于x的不等式
難點 不等式的綜合應用
不等式是繼函數與方程之后的又一重點內容之一,作為解決問題的工具,與其他知識綜合運用的特點比較突出。不等式的應用大致可分為兩類:一類是建立不等式求參數的取值范圍或解決一些實際應用問題;另一類是建立函數關系,利用均值不等式求最值問題、本難點提供相關的思想方法,使考生能夠運用不等式的性質、定理和方法解決函數、方程、實際應用等方面的問題。
●難點磁場
設二次函數f(x)=ax2+bx+c(a>0),方程f(x)-x=0的兩個根x1、x2滿足0
(1)當x∈[0,x1 時,證明x
(2)設函數f(x)的圖象關于直線x=x0對稱,證明:x0< 。
【數學三角函數教學設計】相關文章:
數學教學設計08-19
數學教學設計01-23
數學教學設計12-22
小學數學教學設計02-18
《用數學》教學設計12-22
數學教學設計:實數10-25
小學數學的教學設計07-31
小學數學教學設計12-19
數學《比的應用》教學設計02-22